Schur マニュアルの問題を解く　その２

6-6節 Exercises 1-3

問１

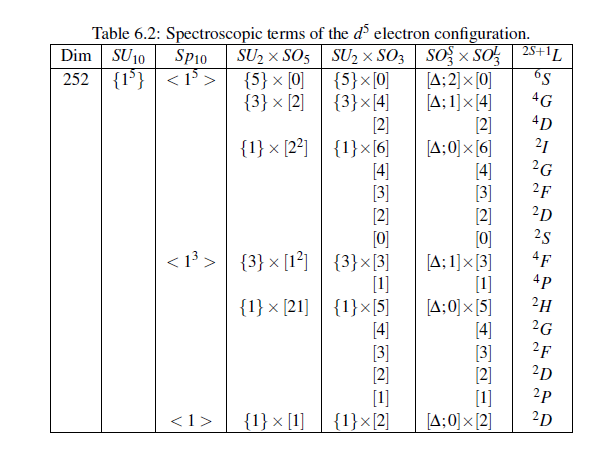
1. The states of the $d^n$ electron configuration may be classified by the following chain of groups
leading, finally, to the spectroscopic terms ${}^{2S+1}L.$ Use SCHUR to establish the results of Table
5.1 for the spectroscopic terms of the $d^5$ configuration
$U_{10} \supset Sp_{10}\supset SU_{2}\times SO_{5}\supset SU_{2}\times SO_{3} \sim SO^S_3\times SO^L_3\equiv {}^{2S+1}L$

f:id:fortran66:20171210124749p:plain

d 電子の分類

SU10 での｛1^5｝表現は、ｄ電子の10個の軌道に5個の電子が反対称に詰まっているということ。Sp10 での分裂は seniority 数に対応（または j-j coupling での軌道の詰め方）、SU2 はスピン角運動量。

ブランチングを求める

ＳＵ１０→Ｓｐ１０
Ｓｐ１０→ＳＵ２×ＳＯ５
ＳＯ５→ＳＯ３

DP> ? tab
 TABleOfBranchingRules
      Format:-
        Modes:- DP
 Description:- Table A.2 : Table of branching rules

NOTES:
Rule No. Group         Subgroup             Rule and number(s) in BRM 
1 :-  U(n)            ->  O(n)                       1,n   
2 :-  U(n)            ->  Sp(n)                      2,n
3 :-  U(n)            ->  U(n-1)                     3,n
4 :-  U(m+n)          ->  U(m) x U(n)                4,m,n
5 :-  U(mn)           ->  U(m) x U(n)                5,m,n
6 :-  U(2k)           ->  U(k)                       6,2k
7 :-  U(n)            ->  SO(3)                      7,n
8 :-  SU(m+n)         ->  U(1) x SU(m) x SU(n)       8,m,n
9 :-  Sp(2k)          ->  SO(3)                      9,2k
10:-  Sp(2k)          ->  U(1) x SU(k)              10,2k
11:-  Sp(2k)          ->  SU(2) x SO(k)             11,2k
12:-  Sp(2k)          ->  U(2k)                     12,2k
13:-  Sp(2k)          ->  U(k)                      13,2k
14:-  Sp(2m+2n)       ->  Sp(2m) x Sp(2n)           14,2m,2n
15:-  Sp(2mn)         ->  Sp(2m) x O(n)             15,2m,n
16:-  S(m+n)          ->  S(m) x S(n)               16,m,n
17:-  S(n)            ->  A(n)                      17,n
18:-  O(n)            ->  S(n)                      18,n
19:-  O(n)            ->  S(n+1)                    19,n
20:-  O(n)            ->  U(n)                      20,n
21:-  O(2k) or O(2k+1)->  U(k)                      21,2k (or 2k+1)    
22:-  O(m+n)          ->  O(m) x O(n)               22,m,n
23:-  O(mn)           ->  O(m) x O(n)               23,m,n
24:-  O(4mn)          ->  Sp(2m) x Sp(2n)           24,2m,2n
25:-  SO(2k+1)        ->  SO(3)                     25,2k+1

DP> brm 
Branch Mode
enter branching & rule numbers> 2 10
U(10) to Sp(10) 
BRM> 1^5
<1^5> + <1^3> + <1>
BRM> stop

enter branching & rule numbers> 11 10
Sp(10) to SU(2) * SO(5) 
BRM> 1^5
{5}[0] + {3}[2] + {1}[2^2]
BRM> 1^3
{3}[1^2] + {1}[21]
BRM> 1
{1}[1]
BRM> stop

enter branching & rule numbers> 25 5
O(5) to SO(3) 
BRM> 0
[0]
BRM> 2
[4] + [2]
BRM> 2^2
[6] + [4] + [3] + [2] + [0]
BRM> 1^2
[3] + [1]
BRM> 21
[5] + [4] + [3] + [2] + [1]
BRM> 1
[2]
BRM> exit

ＳＵ２表現からスピン角運動量へ

SU2xSO3 →SO3xSO3 の自己同型　

DPrep Mode (with function)
DP> gr 2 su2,so3
Groups are SU(2) * SO(3)
DP> au gr1so3, [5*0]
Groups are SO(3) * SO(3)
[s;2][0]
DP> gr 2 su2,so3
Groups are SU(2) * SO(3)
DP> au gr1so3, [3*4]
Groups are SO(3) * SO(3)
[s;1][4]
DP> gr 2 su2,so3
Groups are SU(2) * SO(3)
DP> au gr1so3, [3*2]
Groups are SO(3) * SO(3)
[s;1][2]
DP> gr 2 su2,so3
Groups are SU(2) * SO(3)
DP> au gr1so3, [1*6]
Groups are SO(3) * SO(3)
[s;0][6]
DP> gr 2 su2,so3
Groups are SU(2) * SO(3)
DP> au gr1so3, [1*4]
Groups are SO(3) * SO(3)
[s;0][4]
DP> gr 2 su2,so3
Groups are SU(2) * SO(3)
DP> au gr1so3, [1*3]
Groups are SO(3) * SO(3)
[s;0][3]
DP> gr 2 su2,so3
Groups are SU(2) * SO(3)
DP> au gr1so3, [1*2]
Groups are SO(3) * SO(3)
[s;0][2]
DP> gr 2 su2,so3
Groups are SU(2) * SO(3)
DP> au gr1so3, [1*0]
Groups are SO(3) * SO(3)
[s;0][0]
DP> gr 2 su2,so3
Groups are SU(2) * SO(3)
DP> au gr1so3, [3*3]
Groups are SO(3) * SO(3)
[s;1][3]
DP> gr 2 su2,so3
Groups are SU(2) * SO(3)
DP> au gr1so3, [3*1]
Groups are SO(3) * SO(3)
[s;1][1]
DP> gr 2 su2,so3
Groups are SU(2) * SO(3)
DP> au gr1so3, [1*5]
Groups are SO(3) * SO(3)
[s;0][5]
DP> gr 2 su2,so3
Groups are SU(2) * SO(3)
DP> au gr1so3, [1*4]
Groups are SO(3) * SO(3)
[s;0][4]
DP> gr 2 su2,so3
Groups are SU(2) * SO(3)
DP> au gr1so3, [1*3]
Groups are SO(3) * SO(3)
[s;0][3]
DP> gr 2 su2,so3
Groups are SU(2) * SO(3)
DP> au gr1so3, [1*2]
Groups are SO(3) * SO(3)
[s;0][2]
DP> gr 2 su2,so3
Groups are SU(2) * SO(3)
DP> au gr1so3, [1*1]
Groups are SO(3) * SO(3)
[s;0][1]
DP> gr 2 su2,so3
Groups are SU(2) * SO(3)
DP> au gr1so3, [1*2]
Groups are SO(3) * SO(3)
[s;0][2]

規約表現の次元を求めて検算

SU10->Sp10
252=132+110+10

Sp10->SU2xSO5
132=6*1+4*14+2*35
110=4*10+2*35
10 = 2*5

SO5->SO3
1=1
14=9+5
35=13+9+7+5+1
10=7+3
35=11+9+7+5+3
5=5

DP> gr sp10
Group is Sp(10)
DP> dim 1^5
missing brackets or group not set?
Dimension = 0
DP> rep
REP mode       
Group is Sp(10)
REP> dim 1^5
dimension = 132
REP> gr u10
Group is U(10)
REP> dim 1^5
dimension = 252
REP> gr sp10
Group is Sp(10)
REP> dim 1^5
dimension = 132
REP> dim 1^3
dimension = 110
REP> dim 1^1
dimension = 10
REP> dim 1^5+1^3+1
dimension = 252
REP> gr su2
Group is SU(2)
REP> dim 5
dimension = 6
REP> dim3
dimension = 4
REP> dim 1
dimension = 2
REP> gr so5
Group is SO(5)
REP> dim 0
dimension = 1
REP> dim 2
dimension = 14
REP> dim 2^2
dimension = 35
REP> dim 1^2
dimension = 10
REP> dim 21
dimension = 35
REP> dim 1
dimension = 5
REP> gr so3
Group is SO(3)
REP> dim0
dimension = 1
REP> dim 4
dimension = 9
REP> dim 2
dimension = 5
REP> dim 6
dimension = 13
REP> dim 4
dimension = 9
REP> dim 3
dimension = 7
REP> dim 2
dimension = 5
REP> dim 0
dimension = 1
REP> dim 3
dimension = 7
REP> dim 1
dimension = 3
REP> dim 5
dimension = 11
REP> dim 4
dimension = 9
REP> dim 3
dimension = 7
REP> dim 2
dimension = 5
REP> dim 1
dimension = 3
REP> dim 2
dimension = 5
REP> gr so3
Group is SO(3)
REP> dim s2
dimension = 6
REP> dim s1
dimension = 4
REP> dim s0
dimension = 2
REP>

問２

2. If two sets of states of a $d^n$ configuration transform under $SO_5$ as the irreducible representations $[\lambda]$ and $[\mu]$ respectively their matrix elements of an operator transforming as $[\nu]$ will certainly vanish unless
$[\lambda]\times[\mu]\supset[\nu]$
The Coulomb interaction within the $d^n$ configuration can be expanded in terms of operators symmetrised with respect to the same groups used to classify the states. One of the relevant operators transforms as $[2^2]$ under $SO_5$ . Let $c([\lambda][\mu][2^2])$ be the number of times $[2^2]$ occurs in the $SO_5$ Kronecker product $[\lambda]\times[\mu]$ . Use SCHUR to construct the entries given in Table 5.2 for the numbers $c([\lambda][\mu][2^2])$ .

Table 5.2 とは、Table 6.3 のことか？　
f:id:fortran66:20171210131733p:plain

rep mode で積を取る

積に関しては可換なので半分だけ計算すればよい。
rep mode での外積は prod

DPrep Mode (with function)
DP> rep
REP mode       
REP> gr so5
Group is SO(5)
REP> compare 22 prod 0,0
zero
REP> compare 22 prod 0,1
zero
REP> compare 22 prod 0,1^2
zero
REP> compare 22 prod 0,2
zero
REP> compare 22 prod 0,21
zero
REP> compare 22 prod 0,2^2
[2^2]
REP> compare 22 prod 1,1
zero
REP> compare 22 prod 1,1^2
zero
REP> compare 22 prod 1,2
zero
REP> compare 22 prod 1,21
[2^2]
REP> compare 22 prod 1,2^2
[2^2]
REP> compare 22 prod 1^2,1^2
[2^2]
REP> compare 22 prod 1^2,2
zero
REP> compare 22 prod 1^2,21
[2^2]
REP> compare 22 prod 1^2,2^2
[2^2]
REP> compare 22 prod 2,2
[2^2]
REP> compare 22 prod 2,21
[2^2]
REP> compare 22 prod 2,2^2
[2^2]
REP> compare 22 prod 21,21
2[2^2]
REP> compare 22 prod 21,2^2
[2^2]
REP> compare 22 prod 2^2,2^2
[2^2]
REP>

問３

3. Show that for $SO_5$ the irreducible representation $[2^2]$ occurs once in the symmetric part of the Kronecker square of the irreducible representation $[2^2]$ and once in the antisymmetric part.

問題がわけわかめ。

d 電子に関わる問題が続いているとして、[2^2] が d^5 のが問１で求めた {1}[2^2] ～[s;0][2^2] のことであるとする。この二乗をとってスピンで分類する。

DP> gr 2 so3,so5
Groups are SO(3) * SO(5)
DP> prod [s0*2^2], [s0,2^2]
mistake.
missing brackets or group not set?
zero
DP> prod [s0*2^2], [s0*2^2]
[1][4^2] + [1][43] + [1][42] + [1][41] + [1][4] + [1][3^2] + [1][32] + [1][31] + [1][3] + [1][2^2] + [1][21] + [1][2] + [1][1^2]
 + [1][1] + [1][0] + [0][4^2] + [0][43] + [0][42] + [0][41] + [0][4] + [0][3^2] + [0][32] + [0][31] + [0][3] + [0][2^2] + [0][21]
 + [0][2] + [0][1^2] + [0][1] + [0][0]
DP>

[1][2^2] spin triplet
[0][2^2] spin singlet が各1個づつ。これでいいのか？