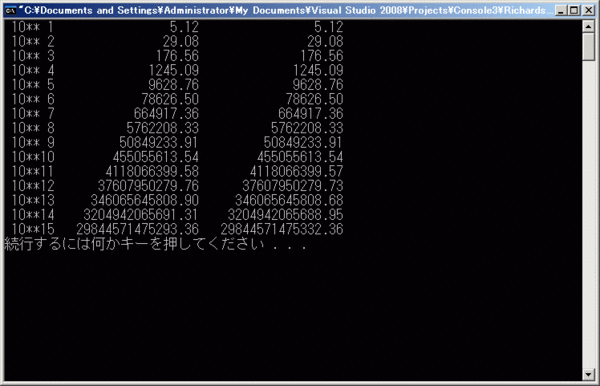
『Extrapolateせよ』と言われると、ヒューゴー・ガーンズバックを思い出してしまう駄目刷り込み。今日も昨晩に続き、積分のRichardson補外(もしくは外挿)をば。
ところでSFといえば映画『涼宮ハルヒの消失』を見てきました。そろそろ劇場も空いてる頃かなと思ったんですが満席でした。
(以下ネタバレ含む)
斬新な演出とかは無かったのですが、原作に忠実に丁寧に作ってありました。『日常+長門』と『異常+ハルヒ』の選択を迫られるキョン君ですが、本当にあれでよかったのか?というか、改変後の世界でのキョン君の言動はほとんど統合失調症ですので、国木田君や朝倉さんはすぐキョン君を適切な病院に入院させてあげて下さい。
見ていて連想が働いたのは、ミケランジェロ・アントニオーニの映画『情事』です。いわゆる「愛の不毛」三部作のひとつです。
こちらでは、ピクニック中に忽焉として消失した女友達を、周囲の人々が初めから居なかったかのように忘れてゆくのに戸惑いながら、女主人公(モニカ・ヴィッティ)が、消失した女友達の行方を、女友達の婚約者と二人であてども無く探しまわるのですが、そのうちにズルズルとその婚約者の男と不倫の関係となり、最初の気持ちとは反対に消えた女友達が消失したままでいて欲しいと願うようになります。しかし、不倫相手の男は、すぐに他の女にちょっかいを出し始めたりして、結局何の救いも無い宙ぶらりんの不安感の中に観客ともども置き去りにされてしまいます。
二つの映画は、消失した女を捜しつつ歪んだ三角関係がこじれてゆくという点で、微妙に準同型な構造を取りながらも、結論が逆ですが、アントニオーニ方向へ進むのは鬱展開としてありふれているので、キョン君の選択でよしかな?
とりあえず、朝倉眉毛さん大活躍でおk!
(ネタバレ終わり)
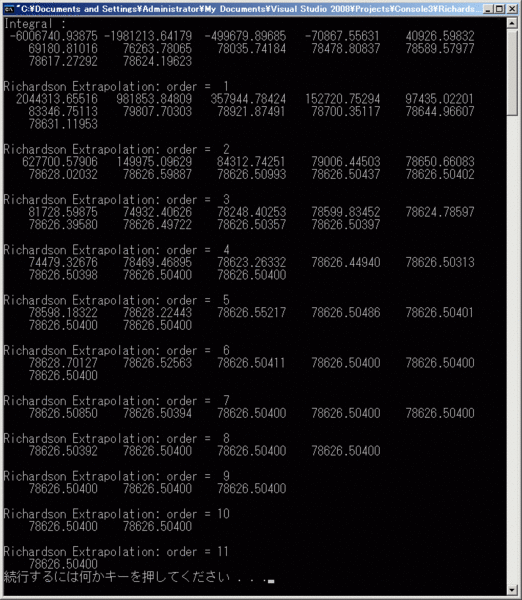
Richardson補外
「なぜ関数プログラミングは重要か」
'84年の段階でこのFORTRAN66式のプログラム例は無いだろwと苦笑しつつ、この中の補外の次数を上げてゆく例題が面白いので、今風のFortranで取り入れてみます。
なお、Fortran2003式のALLOCATABLE配列の自動際割付を有効化するために、Intel Fortranでは/assume:realloc_lhsの追加オプションが必要です。
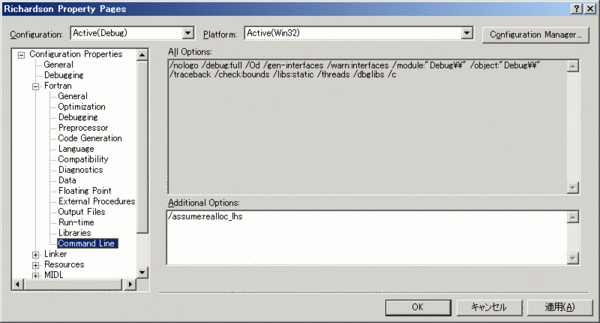
ソースプログラム
昨日のプログラムを少し改変しただけなので、余り深く考えていません。
追記H22-2-20:Internal procedureを引数にすることは、ISOの規格では禁止だそうです。規格にのっとるには全部をModuleに納めて外部にくくりだすことが必要でしょう。
PROGRAM gauss IMPLICIT NONE INTEGER, PARAMETER :: kd = SELECTED_REAL_KIND(14) INTEGER :: k DO k = 1, 15 PRINT '(a, i2, 2F20.2)', ' 10**', k, gauss_Li(12, k, trapezoid), gauss_Li(12, k, simpson) END DO STOP CONTAINS REAL(kd) FUNCTION gauss_Li(n, k, func) INTEGER, INTENT(IN) :: n, k INTERFACE REAL(kd) FUNCTION func(x0, x1, k) IMPORT REAL(kd), INTENT(IN) :: x0, x1 INTEGER, INTENT(IN) :: k END FUNCTION func END INTERFACE REAL(kd) :: x0, x1 REAL(kd), ALLOCATABLE :: y(:) INTEGER :: i, j x0 = LOG( 2.0_kd) x1 = LOG(10.0_kd**k) y = f(x1) - f(x0) - [( func(x0, x1, 2**i), i = 1, n )] DO j = 1, n - 1 y = [( richardson(y(i), y(i + 1), j), i = 1, SIZE(y) - 1 )] END DO gauss_Li = y(1) RETURN END FUNCTION gauss_Li REAL(kd) ELEMENTAL FUNCTION richardson(x0, x1, k) REAL(kd), INTENT(IN) :: x0, x1 INTEGER, INTENT(IN) :: k richardson = (x1 - x0 / 2.0_kd**k) / (1.0_kd - 1.0_kd / 2.0_kd**k) RETURN END FUNCTION richardson REAL(kd) ELEMENTAL FUNCTION trapezoid(x0, x1, n) REAL(kd), INTENT(IN) :: x0, x1 INTEGER, INTENT(IN) :: n REAL(kd) :: h INTEGER :: i h = (x1 - x0) / n trapezoid = h * ( 0.5_kd * ( f(x0) + f(x1) ) + SUM([( f(x0 + i * h), i = 1, n - 1 )]) ) RETURN END FUNCTION trapezoid REAL(kd) ELEMENTAL FUNCTION simpson(x0, x1, n) INTEGER, INTENT(IN) :: n REAL(kd), INTENT(IN) :: x0, x1 REAL(kd) :: h, odd, even INTEGER :: i h = (x1 - x0) / n odd = SUM([( f(x0 + i * h), i = 1, n , 2 )]) even = SUM([( f(x0 + i * h), i = 2, n - 2, 2 )]) simpson = h / 3.0_kd * ( f(x0) + f(x1) + 4.0_kd * odd + 2.0_kd * even ) RETURN END FUNCTION simpson REAL(kd) ELEMENTAL FUNCTION f(x) REAL(kd), INTENT(IN) :: x f = EXP(x) * LOG(x) RETURN END FUNCTION f END PROGRAM gauss