整数の分割

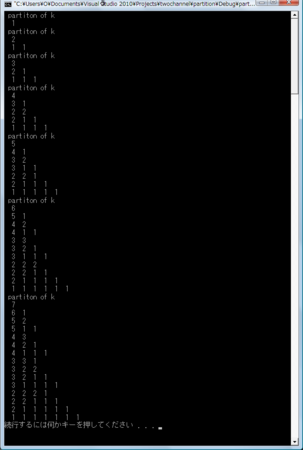
以前整数の分割数 p(n) を漸化式によって求めましたが、今回は分割そのものを求めることにします。
再帰を使った導出法は、富田氏による 『Fortran90プログラミング』例題8.10を参考としました。

以下のプログラムでは、配列生成子 [ ] を用いて、サブルーチンの引数をスタックのように利用しています。とても短く記述できるので大変便利です。メインプログラムでは、大きさ０のダミー配列を与えればいいのですが、配列生成子 [ ] ではサイズ 0 の配列を生成できないようなので、無意味ながらサイズ 0 の配列を宣言しておきました。
追記：[integer::] とやれば可能でした。配列生成子に型を与えないと何の配列か分からないので、当然気づくべきでした。

実行結果

ここでは 1 から 7 までの分割を示しています。一応 20 までの分割の個数が以前の漸化式の結果と一致することを確かめました。

ソース・プログラム

module m_partition
    implicit none
contains
    recursive subroutine partition(list, n, n0)
      integer, intent(in) :: list(:), n, n0
      integer :: i
      if (n == 0) then
        write(*, '(25i3)') list
      else 
        do i = n - n0, n - 1
          call partition([list, n - i], i, min(i, n - i))
        end do
      end if
      return
    end subroutine partition
end module m_partition
    
program part
    use m_partition
    implicit none
    integer :: k
    do k = 1, 7
      print *, 'partiton of k'
      call partition([integer::], k, k)
    end do
    stop
end program part