Quick sort + Bubble sort

Quick sortは、要素数が少ないときはかえって遅いので、要素数が減ったところでBubble sortのような素朴な方法に切り替えたほうが効率がよくなります。

ここではBubble sortそのものではないのですが(しいて言えば沈殿sort?)、同等なO(N^2)のSORTを要素数５０以下の時に用いることにします。

必要なコンパイラ・オプション
/assume:realloc_lhs　
/heap-arrays100000

■実行結果

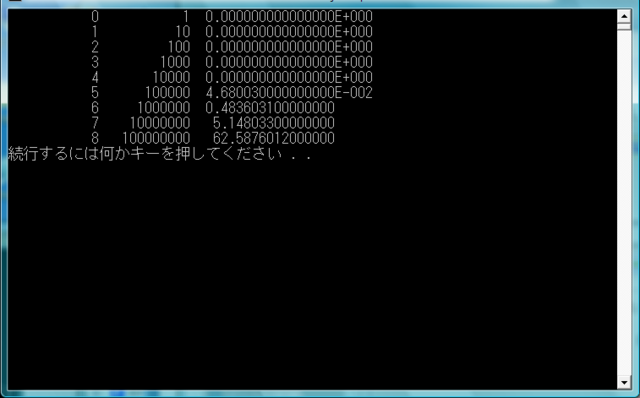
要素数１までQuickSortを用いたものに比べて、ファクター２で高速になりました。全体としての必要時間がO(n*Log(n))になっていることには変わりありません。

■原始プログラム

MODULE m_sort
  IMPLICIT NONE
 CONTAINS
!
  RECURSIVE PURE FUNCTION qsort(x) RESULT(res)
    REAL, ALLOCATABLE :: res(:)
    REAL, INTENT(IN) :: x(:)
    
    IF (SIZE(x) <= 50) THEN
      res = n2sort(x)
    ELSE
      res = [ qsort( PACK(x(2:), x(2:) <  x(1)) ), x(1), qsort( PACK(x(2:), x(2:) >= x(1)) ) ]
    END IF

    RETURN
  END FUNCTION qsort

  PURE FUNCTION n2sort(x)
    REAL, ALLOCATABLE :: n2sort(:)
    REAL, INTENT(IN) :: x(:)
    REAL :: tmp
    INTEGER :: i, j
    
    n2sort = x
    DO i = 1, SIZE(x)
     DO j = i + 1, SIZE(x)
      IF ( n2sort(i) > n2sort(j) ) THEN
        tmp       = n2sort(i)
        n2sort(i) = n2sort(j)
        n2sort(j) = tmp
      END IF    
     END DO
    END DO
    
    RETURN
  END FUNCTION n2sort

END MODULE m_sort
!========================================================
PROGRAM sort
 USE m_sort
  IMPLICIT NONE
  REAL, ALLOCATABLE :: x(:), y(:)
  REAL(8) :: t0, t1
  INTEGER :: i

  CALL RANDOM_SEED()
  DO i = 0, 8
    ALLOCATE( x(10**i) )
    CALL RANDOM_NUMBER(x)
    CALL CPU_TIME(t0)
    y = qsort(x)
    CALL CPU_TIME(t1)
    PRINT *, i, 10**i, t1 - t0
    DEALLOCATE( x, y )
  END DO

  STOP
END PROGRAM sort