Hilbert matrix 1958

[Fortran66] 1958年のプログラムがほとんど無修正で動く件

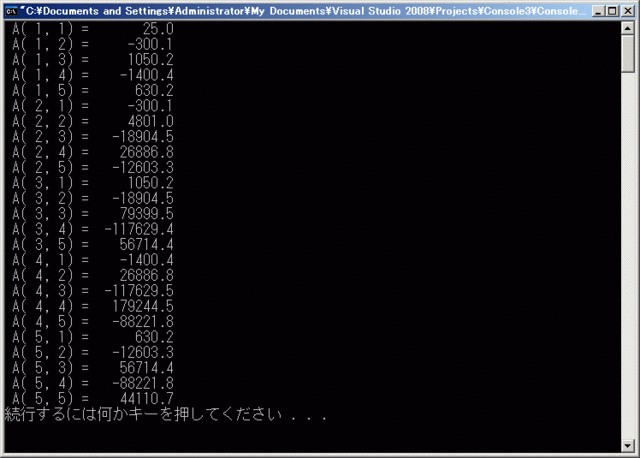
計算機歴史博物館のサイトにFortran関連の古文書が置かれているのですが、その中に1958年にFORTRANで書かれた、５＊５のHilbert行列の逆行列を掃き出し法で求めるプログラムがありました。

このプログラムは現在のコンパイラでも、ほとんど無修正で動きます。わずかな修正点は、今で言うコンパイラ指示行に当たるFREQUENCY命令をコメントアウトすること、整数を実数に変換する命令をFLOATFからFLOATにすること、プログラムの終了を表すEND命令を加えることです。

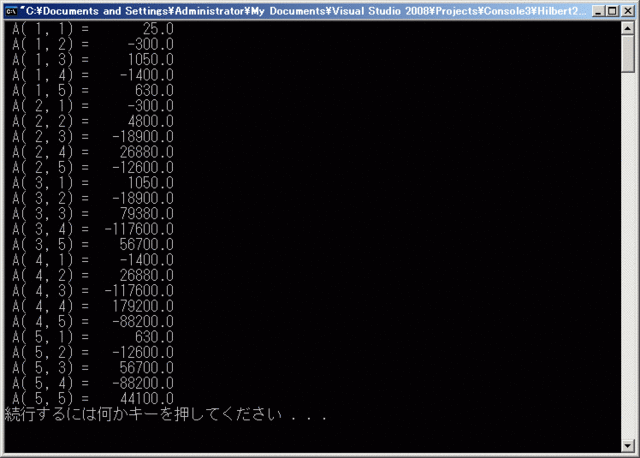
実行結果の数値は、結構違いがありますが、Hilbert行列（ $H_{ij}={1\over{i + j - 1}}$ ）は逆行列が求まりにくい、たちの悪い行列として知られている点と、IBMのFORTRANは16進浮動小数点を用いていた点（FORTRAN Iでもそうなのかは確かめてませんが）を鑑みると、誤差のうちと考えられます。

50年以上も前のコードがほとんどそのまま動くFortranは気持ちいですね。上代・中世・近世・現代の国語を全部包括しているようなものです。

なお、固定フォーマットのFORTRANプログラムは、空白が無視されますので、S T O P のように命令を空白で区切ってもSTOPの意味となります。Fortran90以降で可能になった自由形式では、空白が区切りとなるので命令語は連続して書かねばなりません。空白をトークンとしている最近の言語とは少し違います。

実行結果

ソースコード

C     MATRIX INVERSION ORDER 5
!     FREQUENCY  6(2,1,2)
      DIMENSION  A(5,5)
      DO 1 I = 1, 5
      DO 1 J = 1, 5
    1 A(I,J) = 1.0/FLOAT(I+J-1)  ! FLOATF -> FLOAT
      DO 5 K = 1, 5
      D = A(K,K)
      A(K,K) = 1.0
      DO 2 J = 1, 5
    2 A(K,J) = A(k,J)/D
      DO 5 I = 1, 5 
    6 IF(I-K) 3,5,3
    3 D = A(I,K)
      A(I,K) = 0.0
      DO 4 J = 1, 5
    4 A(I,J) = A(I,J) - D * A(K,J)
    5 CONTINUE
      DO 246 I = 1,5
      DO 246 J = 1,5
  246 PRINT 247,I, J, A(I,J)
  247 FORMAT (3H A(I2,1H,I2,4H) = F10.1,I1)
           S     T     O     P
      END

FORMATの尻に余計なI1がついている。

今風に書いたもの

PROGRAM Hilbert
   IMPLICIT NONE
   INTEGER, PARAMETER :: kd = SELECTED_REAL_KIND(8)
   REAL(kd) :: a(5, 5), d
   INTEGER :: i, j, k

   a = RESHAPE( [((1.0_kd / REAL(i + j - 1, kd), i = 1, 5), j = 1, 5)], [5, 5] )
   
   DO k = 1, 5
     d = a(k, k)
     a(k, k) = 1.0_kd
     a(k, :) = a(k, :) / d
     DO i = 1, 5
       IF (i == k) CYCLE
       d = a(i, k)
       a(i, k) = 0.0_kd
       a(i, :) = a(i, :) - d * a(k, :)
     END DO
   END DO  

   PRINT '(" A(", I2, ",", I2, ") = ", F10.1)', ((i, j, a(i, j), j = 1, 5), i = 1, 5)

   STOP    
END PROGRAM Hilbert