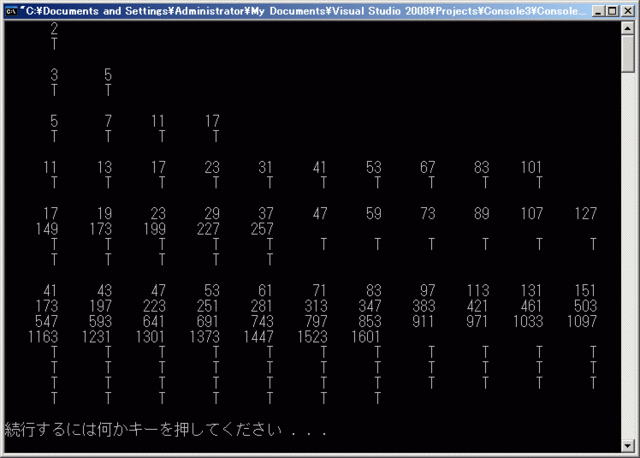
オイラーの素数生成式

オイラーの素数生成式とその類似に基づいて素数を生成し、それが本当に素数かチェックします。素数判定は、素数が小さいので素朴に余りを見てゆくことにします。

オイラーの素数生成式を初めて知った時、随分と妙なものがあるものだと思いましたが、その仲間はそれほど多くないようです。

ELEMENTALな属性がユーザー定義関数でできるようになった今、Fortranでも[1..n]のような形でダミー変数無しで整数配列を生成できると便利かもしれません。現在、[(i, i = 1, n)]の形になりますが、内包式{i|i = 1..n}と思えばありかなとも思えます・・・

出力

ソースコード

PROGRAM test
  IMPLICIT NONE
  INTEGER, PARAMETER :: ieuler(6) = [ 2, 3, 5, 11, 17, 41 ]
  INTEGER :: i, j

  DO i = 1, SIZE(ieuler)
   PRINT '(11I7)',          iprimgen( [(j, j = 1, ieuler(i) - 1)], ieuler(i))
   PRINT '(11L7)', isprime( iprimgen( [(j, j = 1, ieuler(i) - 1)], ieuler(i)) ) 
   PRINT *
  END DO

  STOP

CONTAINS
  
  INTEGER ELEMENTAL FUNCTION iprimgen(n, k)
    INTEGER, INTENT(IN) :: n, k
    iprimgen = n * (n - 1) + k
    RETURN
  END FUNCTION iprimgen
  
  LOGICAL ELEMENTAL FUNCTION isprime(n)
    INTEGER, INTENT(IN) :: n
    INTEGER :: i
    isprime = ALL( MOD(n, [(i, i = 2, n - 1)]) /= 0 )
    RETURN
  END FUNCTION isprime
    
END PROGRAM test